Automatically Unsubscribe from Emails in Rails (and Control Email Preferences)

In this tutorial, I’ll show you how to add a link to any Rails Mailer that will allow a user to automatically unsubscribe from that email. As an added bonus, we’ll build a page allowing a user to update their email preferences across all mailers.

Inspired by GoRails.

Click to expand

Step 1: Build Mailers

Generate mailers.

rails g mailer marketing promotion
rails g mailer notification notify

Update previews by passing a user into the mailer. This assumes your database has at least one user record.

# test/mailers/previews/marketing_mailer_preview.rb

class MarketingMailerPreview < ActionMailer::Preview
  def promotion
    MarketingMailer.with(user: User.first).promotion
  end
end

# test/mailers/previews/notification_mailer_preview.rb

class NotificationMailerPreview < ActionMailer::Preview
  def notify
    NotificationMailer.with(user: User.first).notify
  end
end

Step 2: Build a Model to Save Email Preferences

Generate the model and migration.

rails g model mailer_subscription user:references subscribed:boolean mailer:string

Add a null constraint to the mailer column, and a unique index on the user_id and mailer columns. This will prevent duplicate records.

class CreateMailerSubscriptions < ActiveRecord::Migration[6.1]
  def change
    create_table :mailer_subscriptions do |t|
      t.references :user, null: false, foreign_key: true
      t.boolean :subscribed
      t.string :mailer, null: false

      t.timestamps
    end

    add_index(:mailer_subscriptions, [:user_id, :mailer], unique: true)
  end
end

What’s Going On Here?

We add null: false to the mailer column to prevent empty values from being saved, since this column is required.

We add a unique index on the user_id and mailer columns to prevent a user from having multiple preferences for a mailer.

Run the migrations.
```
rails db:migrate
```

Build the MailerSubscription model.

# app/models/mailer_subscription.rb

class MailerSubscription < ApplicationRecord
  belongs_to :user

  MAILERS =
    OpenStruct.new(
      items: [
        {
          class: "MarketingMailer",
          name: "Marketing Emails",
          description: "Updates on promotions and sales.",
        },
        {
          class: "NotificationMailer",
          name: "Notification Emails",
          description: "Notifications from the website.",
        },
      ],
    ).freeze

  validates :subscribed, inclusion: [true, false], allow_nil: true
  validates :mailer, presence: true
  validates :mailer, inclusion: MAILERS.items.map { |item| item[:class] }
  validates :user, uniqueness: { scope: :mailer }

  # @mailer_subscription.details
  # => [{:class => "MarketingMailer", :name => "Marketing Emails", :description => "Updates on promotions and sales."}]
  def details
    MailerSubscription::MAILERS.items.select { |item| item[:class] == mailer }
  end

  # @mailer_subscription.name
  # => "Marketing Emails"
  def name
    details[0][:name]
  end

  # @mailer_subscription.name
  # => "Updates on promotions and sales."
  def description
    details[0][:description]
  end

  # @mailer_subscription.name
  # => "Subscribe to"
  def action
    subscribed? ? "Unsubscribe from" : "Subscribe to"
  end

  # @mailer_subscription.name
  # => "Subscribe to Marketing Emails"
  def call_to_action
    "#{action} #{name}"
  end
end

What’s Going On Here

We add a constant to store a list of mailers a user will be able to subscribe/unsubscribe from. The class value must match the name of a Mailer class.

We use the values stored in the constant to constrain what values can be set on the mailer column. This prevents us from accidentally creating a record with an invalid mailer.

We add a uniqueness validator between the user and mailer. This is made possible by the unique index we created in the migration. This will ensure a user cannot have multiple preferences for the same mailer.

We use the values stored in the constant to create a variety of helper methods that can be used in views.

Add method to check if a user is subscribed to a specific mailer.

# app/models/user.rb

class User < ApplicationRecord
  has_many :mailer_subscriptions, dependent: :destroy

  # @user.subscribed_to_mailer? "MarketingMailer"
  # => true
  def subscribed_to_mailer?(mailer)
    MailerSubscription.find_by(
      user: self,
      mailer: mailer,
      subscribed: true,
    ).present?
  end
end

What’s Going On Here?

We add a method that checks if a user is subscribed to a particular mailer. If the method finds a matching record, then the user is subscribed. Otherwise, they are not. Note that this is an opt-in strategy. We’re deliberately looking for records where subscribed is set to true. This means that if there is no record in the database, they’ll be considered unsubscribed.

To make this an opt-out strategy, you could simply replace subscribed: true with subscribed: false.

Step 3: Allow a User to Automatically Unsubscribe from a Mailer

Generate a controller to handle automatic unsubscribes.

rails g controller mailer_subscription_unsubcribes

# config/routes.rb

Rails.application.routes.draw do
  ...
  resources :mailer_subscription_unsubcribes, only: %i[show update]
end

Build the endpoints.

# app/controllers/mailer_subscription_unsubcribes_controller.rb

class MailerSubscriptionUnsubcribesController < ApplicationController
  before_action :set_user, only: %i[show update]
  before_action :set_mailer_subscription, only: %i[show update]

  def show
    if @mailer_subscription.update(subscribed: false)
      @message = "You've successfully unsubscribed from this email."
    else
      @message = "There was an error"
    end
  end

  def update
    if @mailer_subscription.toggle!(:subscribed)
      redirect_to root_path, notice: "Subscription updated."
    else
      redirect_to root_path, notice: "There was an error."
    end
  end

  private

  def set_user
    @user = GlobalID::Locator.locate_signed params[:id]
    @message = "There was an error" if @user.nil?
  end

  def set_mailer_subscription
    @mailer_subscription =
      MailerSubscription.find_or_initialize_by(
        user: @user,
        mailer: params[:mailer],
      )
  end
end

Build the view.

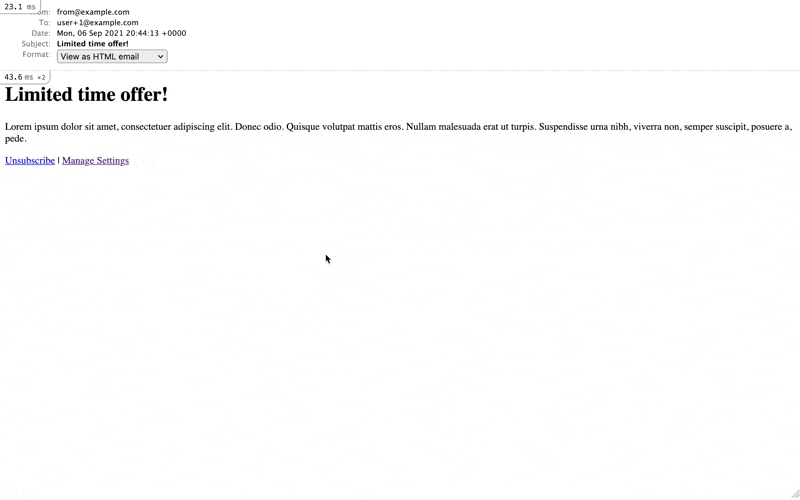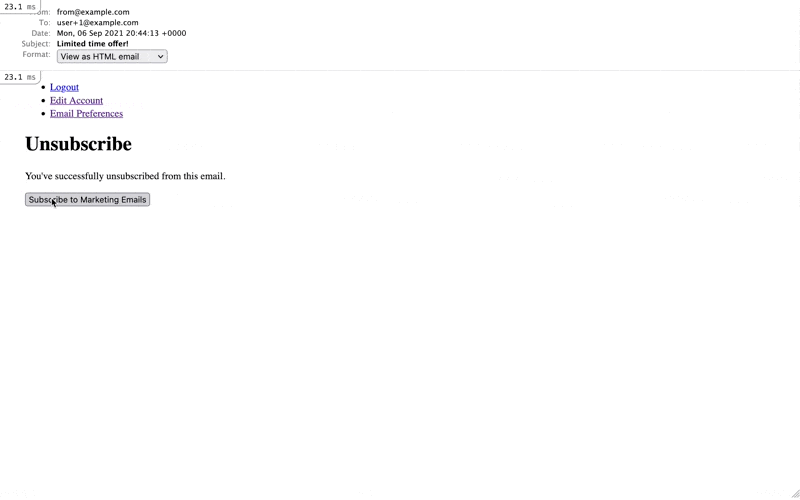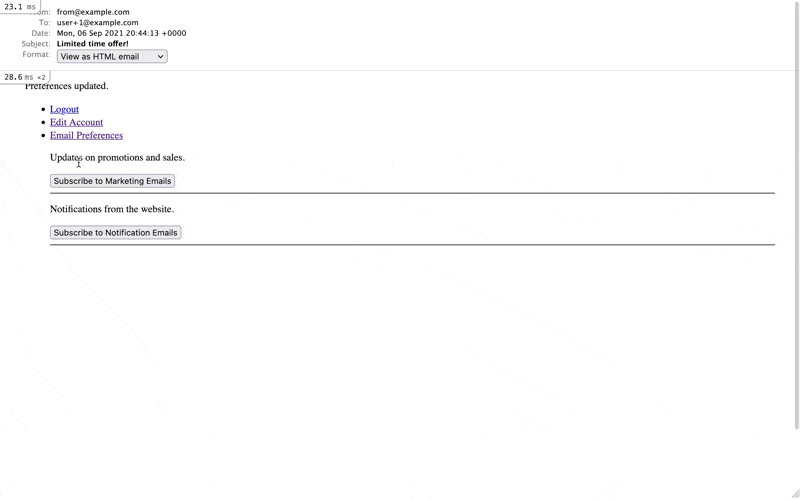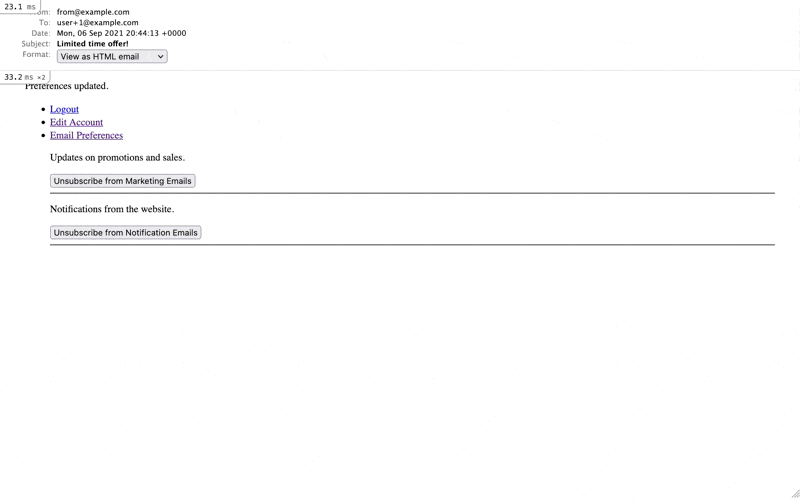
<%# app/views/mailer_subscription_unsubcribes/show.html.erb %>
<h1>Unsubscribe</h1>
<p><%= @message %></p>

<%= button_to @mailer_subscription.call_to_action, mailer_subscription_unsubcribe_path, method: :patch, params: { mailer: params[:mailer] } if @mailer_subscription.present? %>

You can test this be getting the Global ID of a user and going to the endpoint.

User.first.to_sgid.to_s

# => "abc123..."

http://localhost:3000/mailer_subscription_unsubcribes/abc123…?mailer=MarketingMailer

Click to expand

What’s Going On Here?

We create an endpoint that will automatically unsubscribe a user from a particular mailer. This is a little unconventional since we’re creating a record on a GET request (instead of a POST request). We’re forced to do this because a user will be clicking a link from an email to unsubscribe. If emails supported forms, we could create a POST request.

We add a button on that page that will allow the user to resubscribe to the mailer. Note that we don’t redirect back to the show action because that would end up unsubscribing the user from the mailer again.

We find the user through their GlobalID in the URL which makes the URLs difficult to discover. Otherwise the URL would just accept the user’s ID which is much easier to guess. This will prevent a bad actor from from unsubscribing a user from a mailer.

Step 4: Build a Page for User to Update Their Email Preferences

Generate a controller for the MailerSubscription model.

rails g controller mailer_subscriptions

# config/routes.rb

Rails.application.routes.draw do
  resources :mailer_subscription_unsubcribes, only: %i[show update]
  resources :mailer_subscriptions, only: %i[index create update]
end

Build the endpoints.

# app/controllers/mailer_subscriptions_controller.rb
class MailerSubscriptionsController < ApplicationController
  before_action :authenticate_user!
  before_action :set_mailer_subscription, only: :update
  before_action :handle_unauthorized, only: :update

  def index
    @mailer_subscriptions = MailerSubscription::MAILERS.items.map do |item|
      MailerSubscription.find_or_initialize_by(mailer: item[:class], user: current_user)
    end
  end

  def create
    @mailer_subscription = current_user.mailer_subscriptions.build(mailer_subscription_params)
    @mailer_subscription.subscribed = true
    if @mailer_subscription.save
      redirect_to mailer_subscriptions_path, notice: "Preferences updated."
    else
      redirect_to mailer_subscriptions_path, alter: "#{@mailer_subscription.errors.full_messages.to_sentence}"
    end
  end

  def update
    if @mailer_subscription.toggle!(:subscribed)
      redirect_to mailer_subscriptions_path, notice: "Preferences updated."
    else
      redirect_to mailer_subscriptions_path, alter: "#{@mailer_subscription.errors.full_messages.to_sentence}"
    end
  end

  private

    def mailer_subscription_params
      params.require(:mailer_subscription).permit(:mailer)
    end

    def set_mailer_subscription
      @mailer_subscription = MailerSubscription.find(params[:id])
    end

    def handle_unauthorized
      redirect_to root_path, status: :unauthorized, notice: "Unauthorized." and return if current_user != @mailer_subscription.user
    end
end

What’s Going On Here?

We create a page allowing a user to subscribe/unsubscribe from all possible mailers that are defined in MailerSubscription::MAILERS. We can’t call @user.mailer_subscriptions because they may not have any records.

We create a handle_unauthorized method to prevent a user from subscribing/unsubscribing another user from mailers. We need to do this because we’re passing in the ID of the MailerSubscription through the params hash which can be altered via the browser.

Build the views.

<%# app/views/mailer_subscriptions/index.html.erb %>

<ul style="list-style:none;">
  <%= render @mailer_subscriptions %>
</ul>

<%# app/views/mailer_subscriptions/_mailer_subscription.html.erb %>
<% if mailer_subscription.new_record? %>

  <li style="margin-bottom: 16px;">
    <p><%= mailer_subscription.description %></p>
    <%= button_to mailer_subscriptions_path, params: { mailer_subscription:  mailer_subscription.attributes } do %>
      <%= mailer_subscription.call_to_action %>
    <% end %>
    <hr/>
  </li>
<% else %>
  <li style="margin-bottom: 16px;">
    <p><%= mailer_subscription.description %></p>
    <%= button_to mailer_subscription_path(mailer_subscription), method: :put do %>
      <%= mailer_subscription.call_to_action %>
    <% end %>
    <hr/>
  </li>
<% end %>

What’s Going On Here?

We loop through each MailerSubscription instance. If it’s a new_record? we create a MailerSubscription. Otherwise, it’s an existing record and we toggle! the subscribed value.

In either case we use a button_to to hit the correct endpoint. Note that when we’re creating a new MailerSubscription we pass mailer_subscription.attributes as params, but we’re only permitting the mailer value in our controller.

http://localhost:3000/mailer_subscriptions

Click to expand

Step 5: Add Unsubscribe Link to Mailer and Prevent Delivery if User Has Unsubscribed

Add shared logic to ApplicationMailer.

# app/mailers/application_mailer.rb
class ApplicationMailer < ActionMailer::Base
  before_action :set_user
  before_action :set_unsubscribe_url, if: :should_unsubscribe?
  before_action :set_mailer_subscriptions_url, if: :should_unsubscribe?

  after_action :prevent_delivery_if_recipient_opted_out, if: :should_unsubscribe?

  default from: 'from@example.com'
  layout 'mailer'

  private

  def prevent_delivery_if_recipient_opted_out
    mail.perform_deliveries = @user.subscribed_to_mailer? self.class.to_s
  end

  def set_user
    @user = params[:user]
  end

  def set_unsubscribe_url
    @unsubscribe_url = mailer_subscription_unsubcribe_url(@user.to_sgid.to_s, mailer: self.class)
  end

  def set_mailer_subscriptions_url
    @mailer_subscriptions_url = mailer_subscriptions_url
  end

  def should_unsubscribe?
    @user.present? && @user.respond_to?(:subscribed_to_mailer?)
  end
end

What’s Going On Here?

We add several action mailer callbacks to the ApplicationMailer in order for this logic to be shared across all mailers.

We call prevent_delivery_if_recipient_opted_out which will conditionally prevent the mailer from being sent if the user is not subscribed to that mailer. This is accomplished by setting mail.perform_deliveries to true or false based on the return value of @user.subscribed_to_mailer? self.class.to_s. Note that calling self.class.to_s will return the name of the mailer (i.e. MarketingMailer).

We call @user.to_sgid.to_s to ensure the the URL is unique and does not contain the user’s id. Otherwise a bad actor could unsubscribe any user from a mailer.

We conditionally call these callbacks with should_unsubscribe? to ensures we’ve passed a user to the mailer.

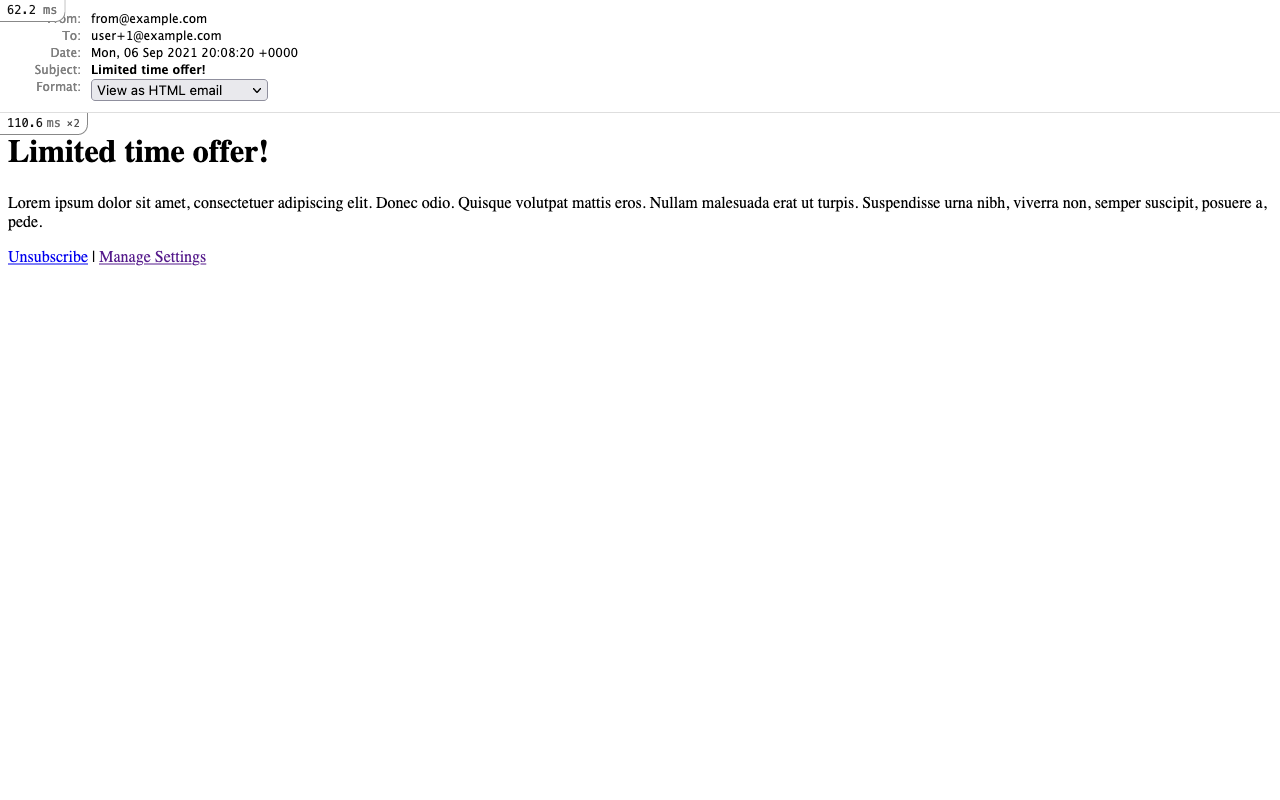
Conditionally render unsubscribe links in mailer layouts.

<%# app/views/layouts/mailer.html.erb %>

<!DOCTYPE html>
<html>
  ...
  <body>
    <%= yield %>
    <%= render "shared/mailers/unsubscribe_links" if @unsubscribe_url.present? %>
  </body>
</html>

<%# app/views/layouts/mailer.txt.erb %>
<%= yield %>
<%= render "shared/mailers/unsubscribe_links" if @unsubscribe_url.present? %>

Click to expand